誰でも分かる技術
誰でも分かる鋳物基礎講座
統計的な考え方からわかること(第4回)
佐藤 万企夫
6 ばらつきに学ぶ
先にわれわれが得るデータは必ずばらつくということを示した。私たちは不良の無い鋳物を造るため、原材料を規定し、全ての工程で作業条件を一定に管理して操業する。しかし結果は思うようにならないから苦労する。現実には、鋳造工程では特に原材料をはじめ製造条件を一定にするということ自体が非常に難しく、操業条件にもある程度のばらつきを認めているからである。ばらつきは人間が行う限り避けることができないものであり、ある程度は認めざるを得ないものである。ここではこのばらつきから何を学ぶことができるかについて少し詳しく説明する。 前者のばらつきを「偶然原因によるばらつき」:避けられないばらつき・・・・① 一般的に、ばらつきが起きる要因として、4M(Man、Machine、Material、Method)を挙げることが多い。これらは絶えず変化するからである。4M以外にMeasure(測定)、Environment(環境)を加えることもある。(第2回、図4参照) 製造した製品の品質の特性値をグラフに記入し、その状態から工程が管理状態にあるか、異常な状態にあるか客観的に判断する道具が管理図である。これを有効に活用することで工程を管理し、品質の維持が図られる。 ①と②の、2つのばらつきについて発生状況を時系列でプロットすると、図82)のようになり、①の場合データはある幅の範囲に入っているが、②の場合は幅から外に出るプロットが発生する。これらの目的とする特性値をプロットし、統計的手法により算出した上部管理限界線(upper control limit line)と下部管理限界線(lower control limit line)の入った管理図を描くことで、工程の状況がわかる。 偶然原因によって起こる品質(特性値)のばらつきは大体一定の分布、通常は大体正規分布している。これを管理されたばらつき(controlled variability)という。管理されたばらつきだけを持つ結果を生ずるような工程の状態を、管理状態、安定状態(controlled state)という。図8の(a)の状態がこれにあたる。 これに対し、工程に異常が起こると、その工程からの結果(特性値)のばらつきが異常に大きくなる。この異常なばらつきを管理されていないばらつき(uncontrolled variability) といい、このようなばらつきを持つ結果を生ずるような工程の状態を、管理されていない状態、不安定状態(uncontrolled state)という。図8の(b)のような状態で、限界から飛び出している点が出るとき、点の並び方にくせがあるときにその工程は管理されていない(out of control)という。 管理図上に描いた管理限界線により、このように起きるばらつきの現象を、感覚ではなく統計的な手法で客観的に判断することができる。 |
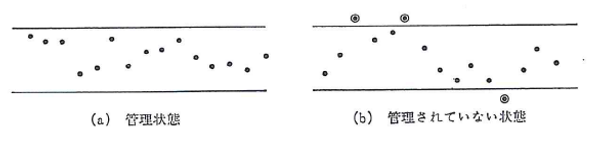 図8 工程から生産された製品の2種のばらつき2) |
| 私たちが通常接する分布は、図92)のようなベル型をした分布、正規分布(normal distribution)に近いものが多い。このような分布を標準偏差で分けると、全体の面積に対する割合がわかる。すなわちランダムサンプリングすると±1σ内のデータが出る確率は約68%、これより外に出る確率は32%となり、±3σ外に出る確率は約0.3%と非常に少ない確率になる。このようなことは通常あまり起こらないので、3σよりデータが外に出たとき、工程が変わったとか工程に何か異常が起きた可能性があると判断することになる。 判断するにあたり気をつけなければいけないこととして、2つのばらつきを判別することであり、確率の概念と2種類の誤りの概念を持つ必要がある。例えばさいころを5回繰返して振ったとき、5回とも奇数が出る確率は(1/2)5、すなわち1/32(=0.03125)である。これは有り得ることで、もし疑うようなことがあればこれを統計学では「第1種の誤り」を犯すという。一方これを当然のように見過ごすことは「第2種の誤り」を犯す可能性がある。私たちが何か判断するとき、常にこの2つの誤りを犯す可能性があるのだということが、統計的判断(検定)の基礎である。 |
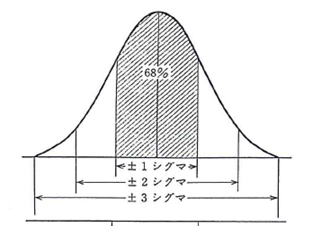 図9 正規分布と確率2) |
| ばらつきのある工程に対して手を打とうとする場合について考える。図102)の管理された分布(A)で、×の点のデータが出たとき、確率が小さいからといって何か異常なばらつきを起こす原因が工程内に起きていると判断すれば、管理されたばらつき(A)であるのに、管理されていないばらつき(B)であると間違えて判断する誤り(第1種の誤りを犯す)がある。一方、工程は平常通り管理されている(A)と判断すれば、実はそのばらつきは工程に異常な原因が起こって、分布の平均値がBのようにずれているのに気づかず見過ごしてしまうという誤り(第2種の誤りを犯す)があるかもしれない。工程は、ばらつく要因の塊(第2回、図4参照)であり、そこから生まれる製品(特性値)は正常に稼働していても必ずばらつくことから、私たちはこの2つの過りを犯す可能性を認めざるを得ない。 |
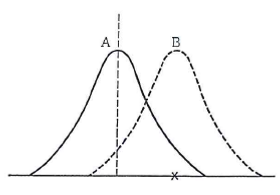 図10 2つの分布と判断2) |
| 2つのばらつきを区分するように引かれた線が管理図中の管理限界線である。これを判断の基準に考えれば、郡内変動に対して3σ、すなわち第1種の誤りを犯す確率は約0.003である。したがって先に述べたサイコロでいうと7~8回連続して奇数が出る確率であり、この線の外にプロットが出るということは、確実に工程内に異常がることを示している。このようなことが起きたら、私たちは直ちに工程に戻り、その原因を徹底的に究明していかなければならない。管理図の管理限界線は、このようにアクションを取るための基準である。 |
7 さいごに
統計的な考え方の重要性について説明したが、私たちは現場において不良が起きたとき、大慌てして起きた不良現象から技術的に考えられるいくつかの対策を行うことで、何とか対策するということが多いのでないかと思う。突発不良に対してはそれでうまくいくこともあるが、慢性的に繰返す不良に対しては簡単にその原因は見つからないことが多い。しかし日常的に現場で得られる様々な要因系データを、取って記録しておくことだけでなく、統計的な手法で日常的に整理していくことで、トラブルが発生する予兆を事前に検知することができる。結果系のデータも、層別して調べることにより何か見えてくるかもしれない。また規格にはいっているからOKという考え方ではなく、ばらつきに注目し、工程能力(Cp)を上げる考え方に移行することが重要である。 |
| 【参考文献】 2)石川 馨著「品質管理入門」、日科技連出版社 |