誰でも分かる技術
誰でも分かる鋳物基礎講座
統計的な考え方からわかること(第2回)
佐藤 万企夫
3 統計的な考え方について
| 私たちは店頭で、例えばSDカードを購入する際に、同じ製品がいくつか陳列されているとき、一般的に手に取り易いものをとってレジに持っていくだろう。これはどの製品をとっても間違いの無い品質レベルであると理解しているからである。ある部品の寿命が、A社製は500時間~5,000時間、B社製の部品は2,000~3,000時間に分布しているとき、価格が同じ場合どちらを選ぶであろうか。図3は30数年ぐらい前の、日本のあるメーカの、日本製とアメリカ製テレビの色の出具合を示す特性値の分布を示したものである。日本製とアメリカ製ともに同じ範囲内に分布しているが、その分布に大きな差があった。範囲を示す線の内側を規格とすれば、日本製に対しアメリカ製は規格内には入っているものの、規格内上限から下限までの製品が一様に分布しており、日本製に比べてばらつきが大きいといえる。このような分布になるのは、製造する工程が不安定である可能性があり、場合によっては全数検査を行うことにより規格外の製品を除去しているかもしれない。 |
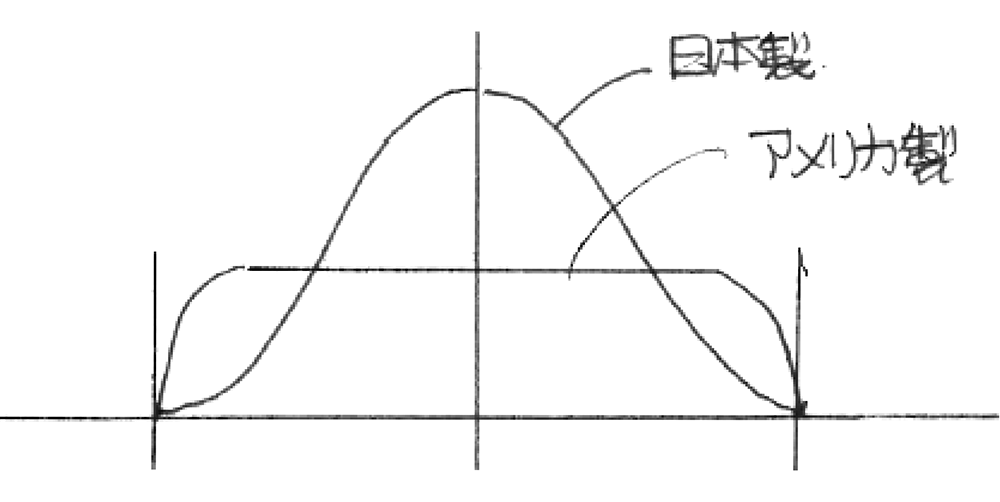 図3 日本製とアメリカ製テレビの色の出具合を示す特性値 |
私たちはこのような場合、ばらつきの少ないB社の部品や日本製の製品を購入するであろう。すなわち集団として、分布としての製品品質の均一なものを選ぶ。 私たちが製造現場でもの(鋳物製品)を造ることを考える。現場は数多くの変動要因に囲まれており、各要因は時々刻々変化している。特に鋳造現場では中子、砂処理、造型、溶解、注湯と、数多くの独立した工程で材料の切り出し・配合から始まり、鋳型を造る砂の性状、造型条件、溶湯の温度や成分、注湯時間や注湯速度等、全ての条件が同じものは皆無であろう。 |
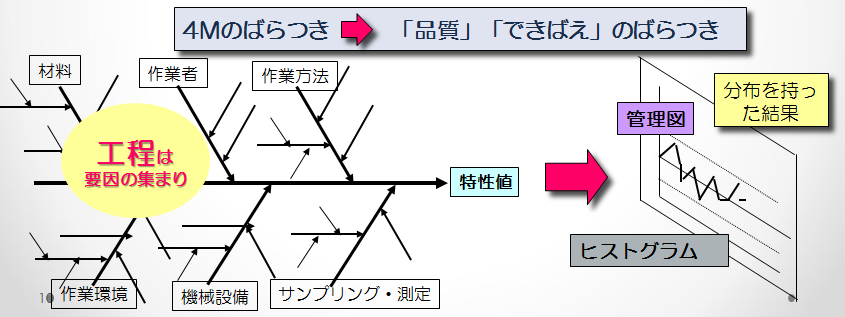 図4 ばらつきの要因とその見え方 |
| ものを作る工程は、図中の特性要因図の一つひとつの矢印に記されたさまざまな要因の集まりであり、そこから生まれる特性値はばらつくということである。この図は「私たちが得るデータは全て一定の1つの値ではなく、ばらついている。工程には科学的にばらつきを与える要因は無限にある。この中で技術的に押さえているのはほんの一部であるから、私たちの工程から生まれる製品がばらつくのは当然である。またサンプリングや測定に誤差はつきものであり、同じものを測定してもデータは必ずばらつく。そしてその結果を管理図やヒストグラムに描くことで何かが見えてくる。」ということを示している。 図5はこの結果を示した管理図であり、本講座の第1回でも紹介した図であるが、一対の管理限界線が入っている。この図は仕事や工程の正常・異常を判断するため、分布がどう変わったかという立場で統計的に判断し、管理するものである。対象の工程等に何か変化(異常)がないかを、すなわち時間的に分布が変わったかどうか、この図に打たれたプロットが示している。図中の(a)点、(b)点のようなものが出ても、下部管理限界線の外に出ていなので通常の変動の範囲内ということで考えればよい。但し、図中(c)のよう、この限界線の外にプロットが出た際には、工程内に何か異常が起きたということで、直ちに工程に戻り異常の原因を究明し、その根本原因を除去する対応をとる必要がある。 |
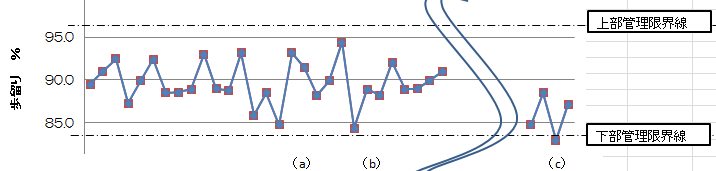 図5 管理図の一例 |
| 仕事の結果をチェックして工程を管理するために、工程内に異常が発見されたらその原因究明を行うが、そのデータがどのような経緯で出てきたのか、すなわちロットやデータの歴史に戻ることであり、それを行うことが層別である。この製品はどのようなプロセス(4M等)の中から生まれてきたのか等を明らかにすることで、原因究明ができる。 統計的な考え方として次の4つを理解するとよい。
|