誰でも分かる技術
誰でも分かる鋳物基礎講座
アルミニウム合金の時効熱処理と析出硬化（第5回）
教授 里 達雄
2 アルミニウム合金の時効熱処理の基礎
（ⅱ）拡散現象
(a)定常状態での拡散
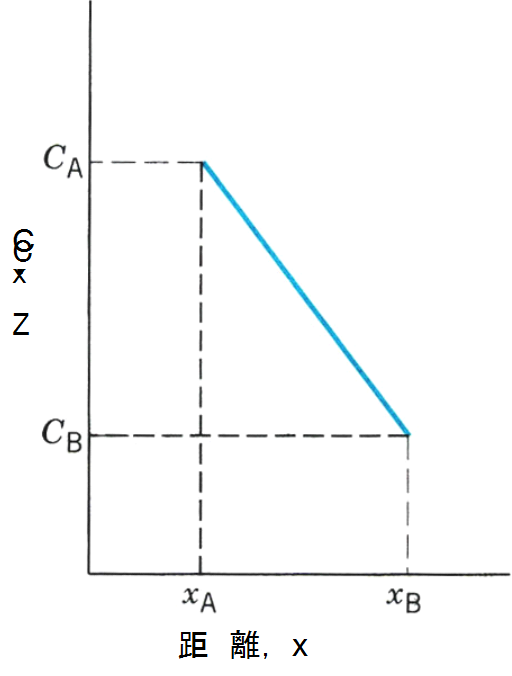
図9 定常状態での原子の拡散と濃度2)
すなわち、
 |
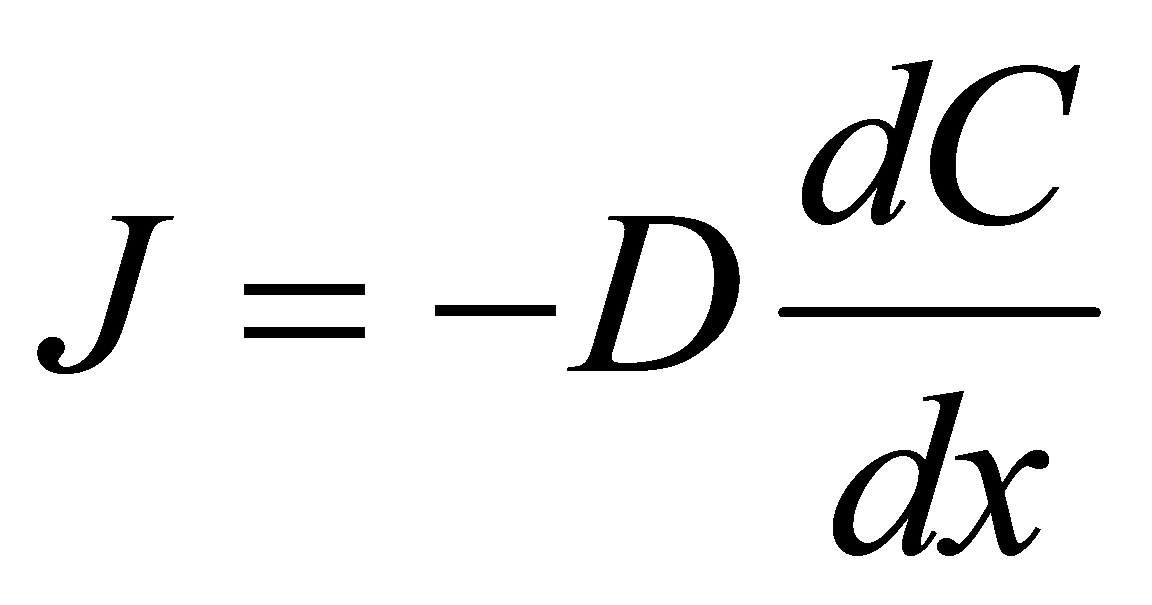(3) |
となる。ここで、Cは位置ｘでの濃度を表わし、Dは拡散係数とよばれる。右辺のマイナスは濃度勾配のプラスと拡散の方向が逆になるためである。式(3)はフィックの第一法則（Fick’s first law）とよばれる。ここでの拡散の駆動力は濃度勾配である。
すなわち、濃度勾配が存在することにより拡散がおこる。
(b) 非定常状態での拡散（補足１）
次に非定常状態の拡散について考える。実際におこる多くの拡散現象はこの非定常状態の拡散である。これはある場所における拡散流および濃度勾配が時間とともに変化する場合である。非定常状態の拡散による濃度の時間変化を図10に示す3)。非定常状態の場合の拡散方程式は、
 |
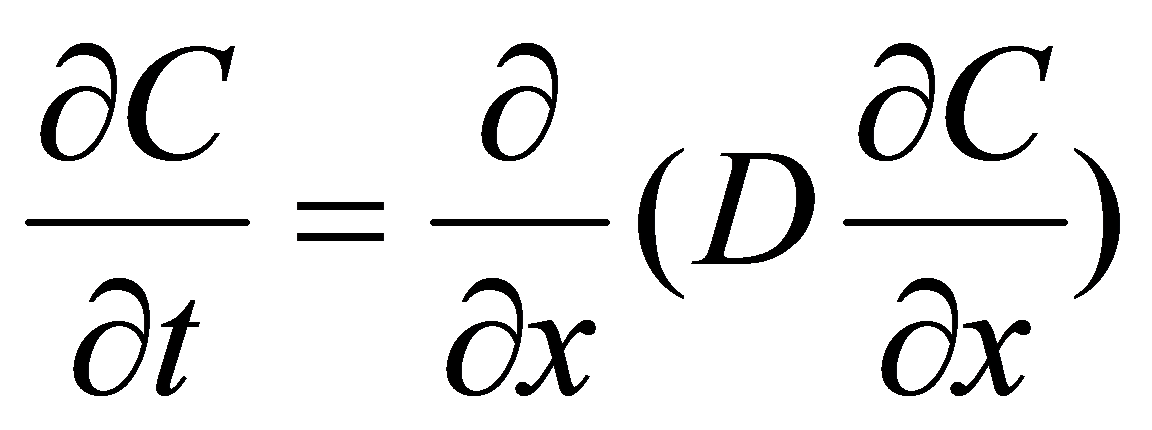(4) |
となる。これは、フィックの第二法則（Fick’s second law）とよばれる。なお、∂記号は偏微分とよばれるものである。
いま、拡散係数Dが濃度依存性をもたないとする（すなわち、拡散係数が濃度によって変化しないとする）と、式(4)は、
 |
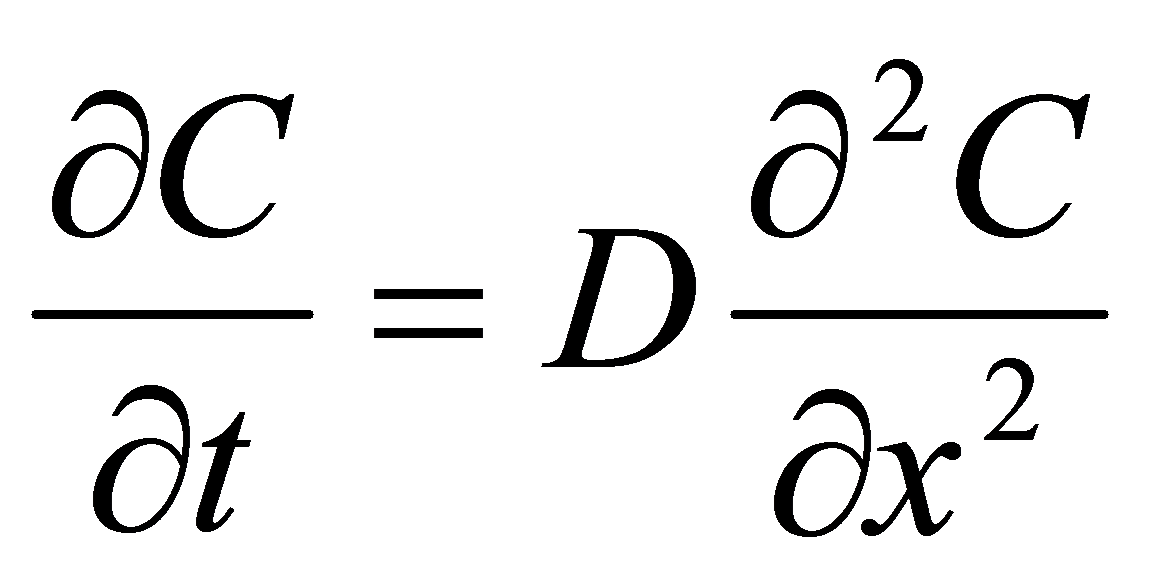(5) |
となる。（図11にFickの第二法則の導出法を参考までに示す）。式(5)の偏微分方程式の解は種々の境界条件で解かれている。実用的にも有用な解は以下のような境界条件の場合である。ここでは解のみを示し、導出過程には触れない。
| (ⅰ) |  |
のとき、 |  |
において |  |
とする。 |
| (ⅱ) |  |
のとき、 |  |
において |  |
|
 |
において |  |
とする。 |
これより、
 |
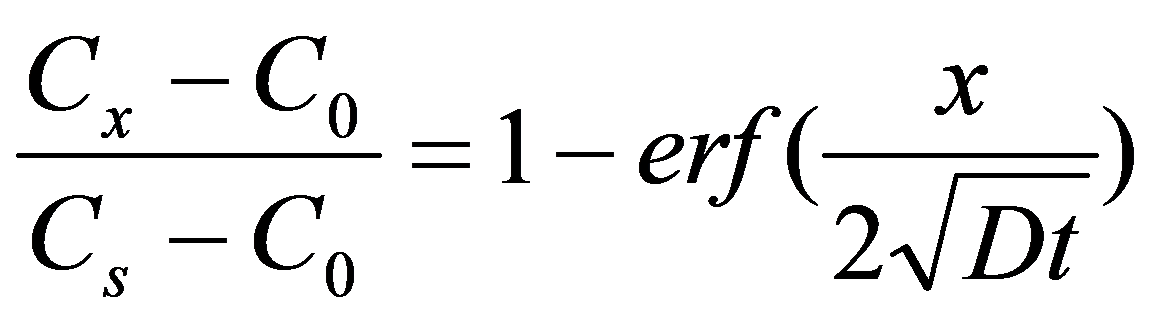(6) |
が解として得られる。ここで、Cxは位置ｘにおける濃度を示す。式(6)の右辺の第2項はガウスの誤差関数であり、
 |
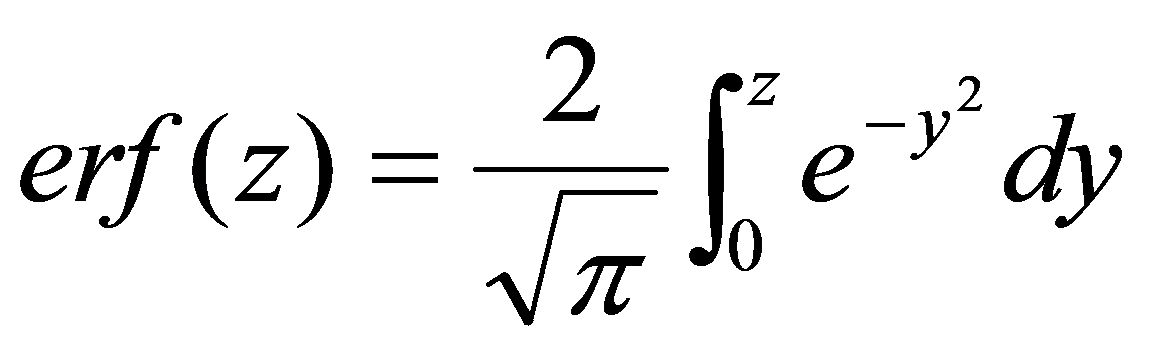(7) |
で定義される。この誤差関数の値をもとに拡散のマスターカーブを図10(b)に示す。すなわち、式(6)から、Cxの値は場所ｘおよび時間ｔの関数として与えられる。具体的には、
の関数となる。
いま、Cx＝C1 となる位置および時間条件について調べると（図10）、
 |
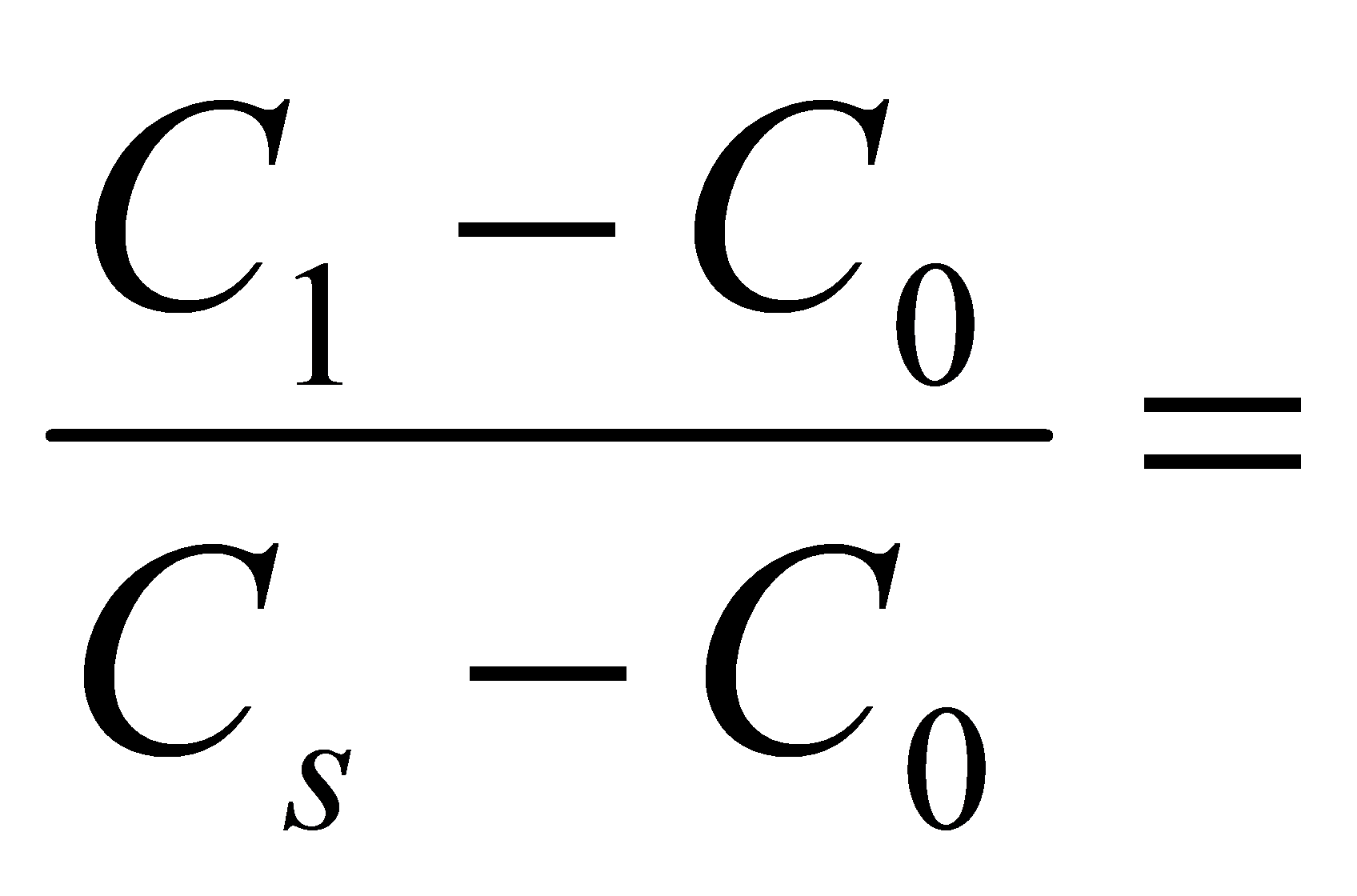一定値 | (8) |
となる。さらに、式(6)より式(8)となるためには、
 |
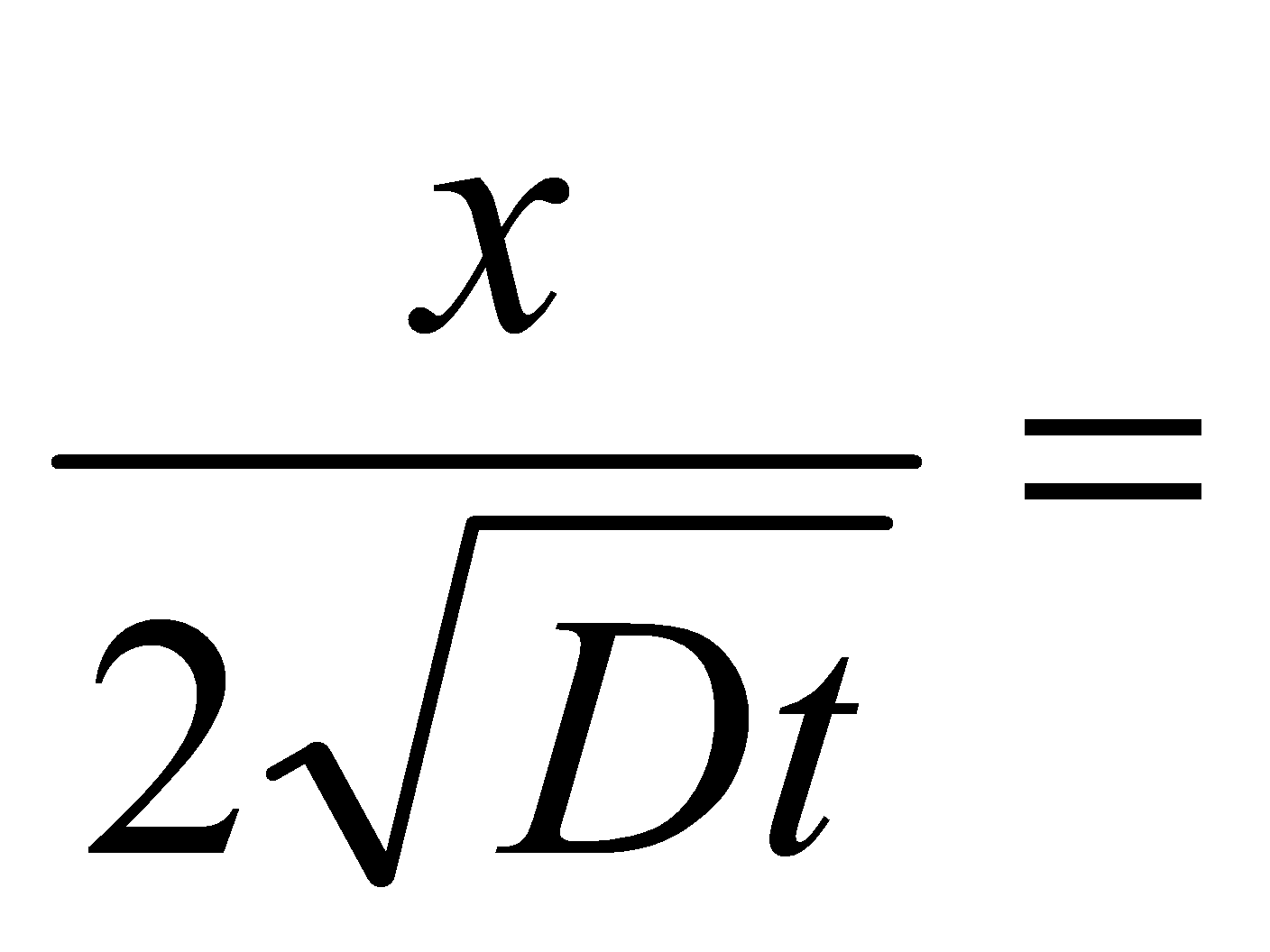一定値 | (9) |
あるいは、
 |
(10) |
の関係が満たされることになる。式(10)は教科書などによく出てくる関係である。図12に拡散による濃度変化を示す4)。いま、濃度C1がCsとC0の中間の値になることを考えると、C1 =(Cs + C0)/2であり、式(8)の一定値は0.5となる。また、
であるため、式(9)で
となり、となる（図12）。また、
の関係を用いると、たとえば、温度T1で時間t1を要する拡散変態につ
いては温度T2で必要となる時間t2を求めることができる。ただし、温度Tでの拡散係数Dが
 |
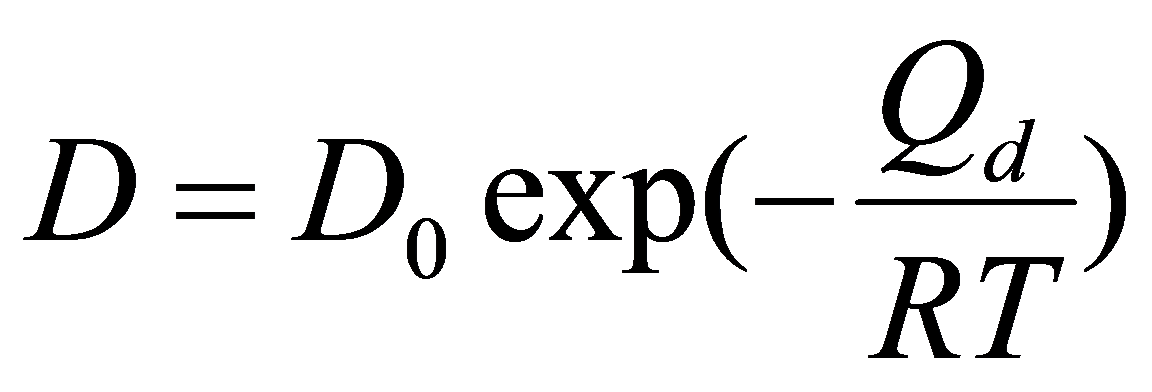(11) |
で与えられるものとする。ここで、D0：振動数項、Qd：拡散の活性化エネルギー、R：ガス定数である。
これより、
 |
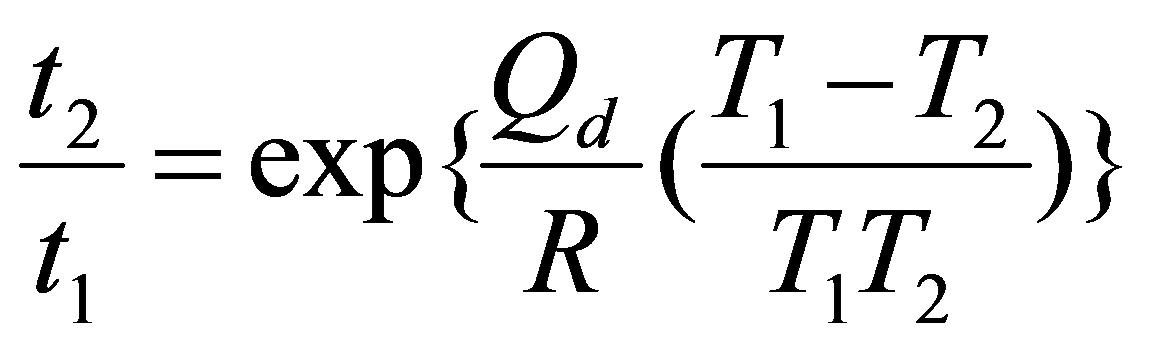(12) |
となる。ただし、T1 < T2とする。なお、導出については図13に示す。
アルミニウムやアルミニウム合金では高温に加熱後、急冷することがよくある。このような場合、熱平衡で存在する濃度よりも高い濃度の空孔が導入される。空孔濃度Cvは一般に、
 |
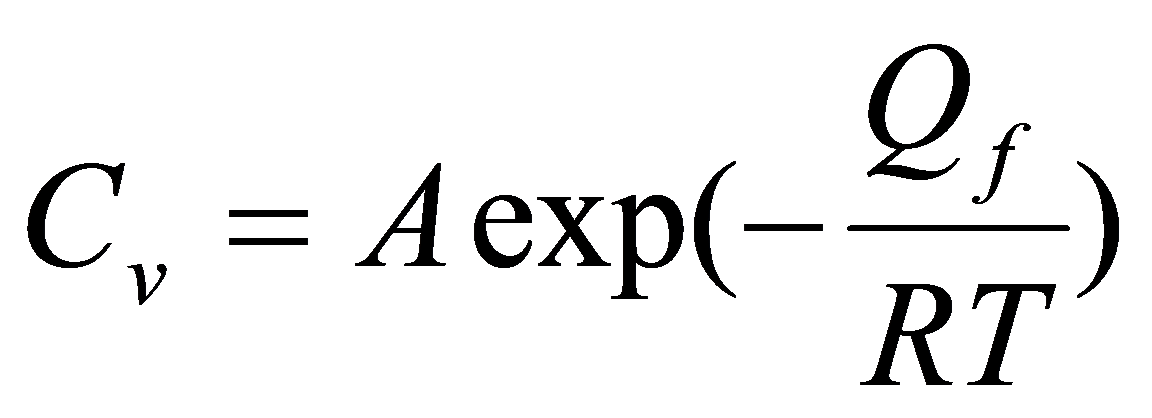(13) |
で与えられる。A : 定数、Qf : 空孔形成の活性化エネルギーである。Cvの温度依存性は図14のようになる5)。すなわち、温度が高くなると空孔濃度は急激に増大する。このような高い濃度の空孔は焼入れなどにより急冷すると消滅せずに残存し、凍結過剰空孔となり、拡散に大きく寄与する。たとえば、低温であっても拡散が急速に進行する。
| （補足１） 非定常状態での拡散の場合，式(4)と式(5)は偏微分方程式で表されており，馴染みがうすい場合にはスキップしても差し支えない．実用的に有用な関係は式(10)である．これにより，拡散の距離と拡散係数および時間との関係を知ることができる．また，濃度プロフィールの時間変化を知りたい場合には式(6)が役に立つ．ここで，ガウスの誤差関数の数値は統計学の教科書などに載っているので，利用できる． |
参考文献
2) W. D. Callister, Jr.: Materials Science and Engineering, An Introduction, John Wiley & Sons, Inc. (1994), 93.
3) J. F. Shackelford: Introduction to Materials Science for Engineers, Prentice-Hall, Inc., (1999), 167.
4) D. A. Porter and K. E. Eastering: Phase Transformations in Metals and Alloys, Chapman & Hall, (1981), p73.
5) 里 達雄: アルミニウム合金の強度（小林俊郎編著）、内田老鶴圃、(2001), p51.
 |
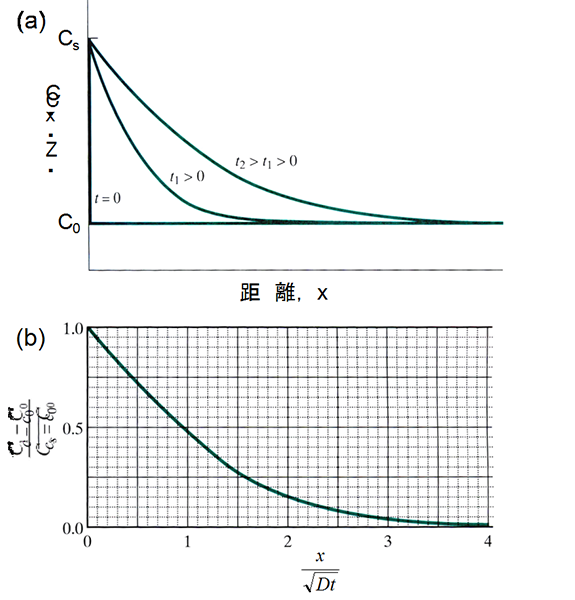| 図10 非定常状態での拡散による濃度変化(a)と規格化した濃度プロフィール(b)3) |
 |
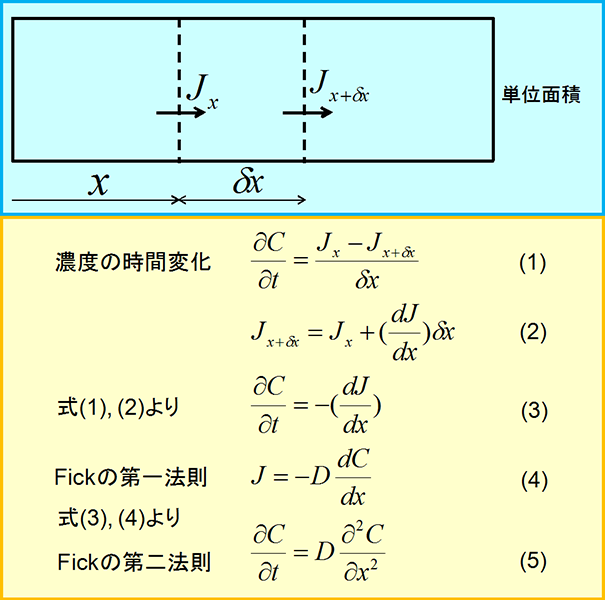| 図11 Fickの第二法則の導出 |
 |
| 図12 拡散による濃度変化。時間は t1, t2, t3と長くなっている。 ただし、Csは変化しないとしている4)。ここで、erf は誤差関数である。 |
 |
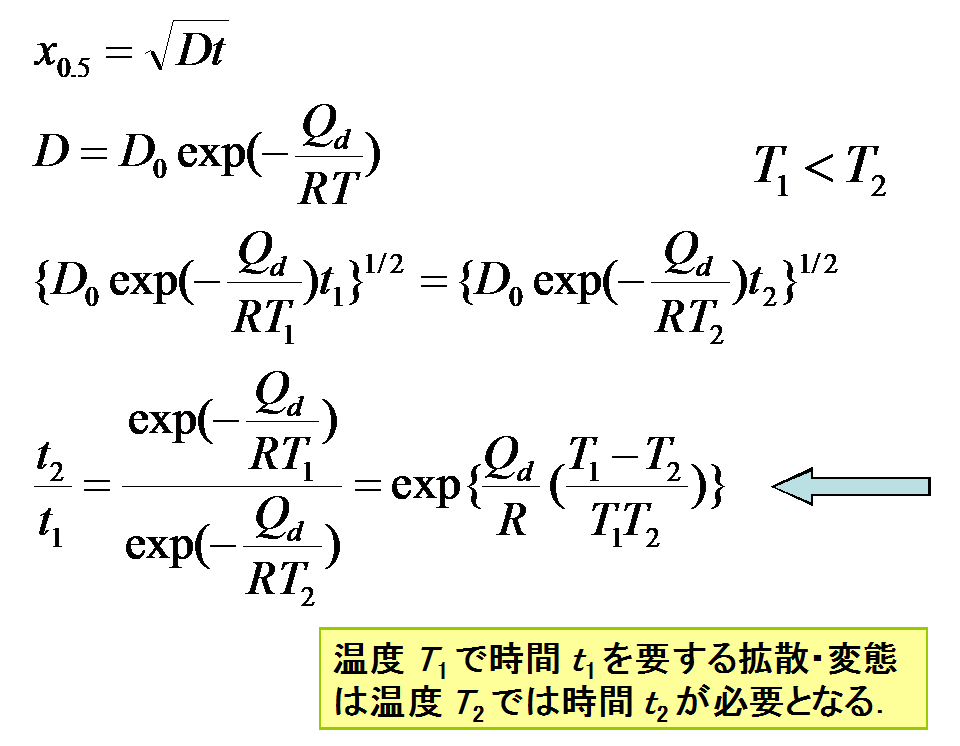| 図13 拡散に関わる現象（均質化・析出など）に要する時間の見積り |
 |
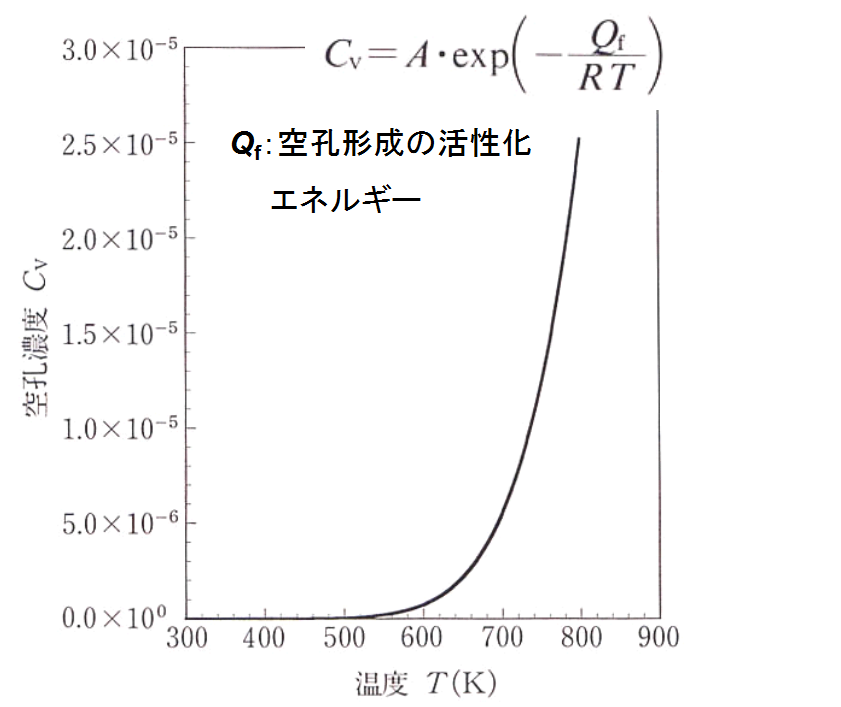| 図14 アルミニウム中の熱平衡空孔濃度 Cv の温度依存性 s |