鋳物でつながるネットワーク、日本鋳造工学会関東支部

アルミニウム合金の時効熱処理と析出硬化（第6回）

2 アルミニウム合金の時効熱処理の基礎

（ⅲ）析出相変態

(a)定常状態での拡散
　図15にA-B二元合金の場合を想定し、平衡状態図とそれに対応する温度Taでのギブズエネルギーを模式的に示す。図15において、濃度Coの合金を温度Tsに保持する（溶体化処理）とα固溶体となり，続いて急冷すると過飽和固溶体となり，これを温度Taに保持する（時効熱処理）とα相が相分解してβ相が析出し，α＋β二相組織となる．これはすでに前述したことである。
　 さて、図15(b)のギブズエネルギーの組成依存性から次のことが分かる。Taにおける組成CoのギブズエネルギーはGoであり、組成Coが組成CαおよびCβのα相およびβ相の二相共存状態になればギブズエネルギーはGfとなり、（線分PQ）だけギブズエネルギーは低下する。ここで、Cα、Cβは共通接線の接点の濃度に対応する（共通接線は平衡の条件から出てくるものである）。はα→α＋βの反応、すなわち、β相が析出する全駆動力となる。

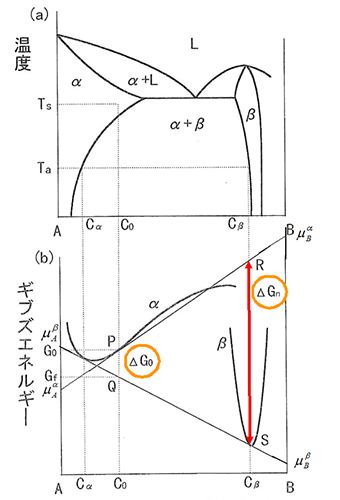図15　A-B二元合金の(a)平衡状態図および(b)ギブズエネルギーの模式図

 (a) 核生成－成長
α相からβ相が析出する初期の核生成について考える．いま，図16に示すように，組成C0のα相中に組成（）のβ相が１モル形成されたときのギブズエネルギー変化を求めてみる．まず，α相中から組成の1モルの粒子を抜き取ったときのギブズエネルギー変化を，次に同じ組成のβ相の1モルの粒子をもどしたときのギブズエネルギー変化をとすると，

	（点Rに対応）	(14)
	（点Sに対応）	(15)

と表される。		：α相中の元素AおよびBの化学ポテンシャル、
		：β相中の元素AおよびBの化学ポテンシャル、
		：β相の元素AおよびBの濃度、である。

従って小さなβ相が核生成することによるギブズエネルギー変化は，

（線分RSに対応）

(16)

と表される。
はβ相の１モルあたりのギブズエネルギー変化であるが，β相の単位体積あたりのギブズエネルギーをとすると，

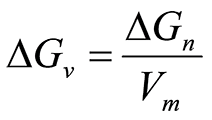(17)

と表すことができる。ここで、はβ相のモル体積（1モルあたりの体積）である。

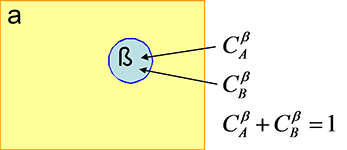図16　α相中におけるβ相の核生成 （凝固のときに液相から固相が晶出するときの取扱いと同じ）

 

(a-1)　均一核生成
上記によって核生成がおこる現象について，溶質原子濃度の熱的ゆらぎによって新しい相（β相）が空間的にランダムに形成される均一核生成と格子欠陥や結晶粒界，介在物，界面などにおこる不均一核生成とがある。
均一核生成の場合，古典的核生成理論に基づけば，α相中に半径rの球状のβ相が形成された場合のギブズエネルギー変化は

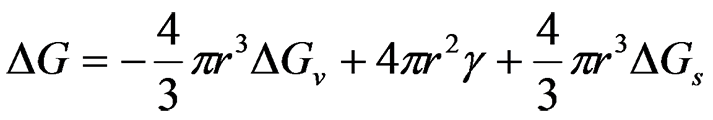(18)

で表される。ここで、はβ相の単位体積あたりの弾性ひずみエネルギー、はα/β界面エネルギーを示す。
は半径rの関数であり、r依存性を図17に示す。はrとともにはじめは増大し、極大を示してから減少する。ここで、極大を与えるrを臨界サイズ，そのときの極大値を障壁エネルギー（あるいは，活性化エネルギー）とよぶ。これらの値は式(18)から、計算することができ、次のようになる。

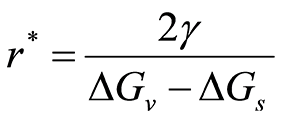		(19)
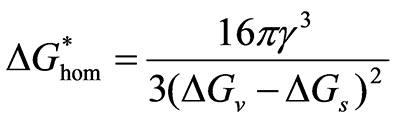		(20)

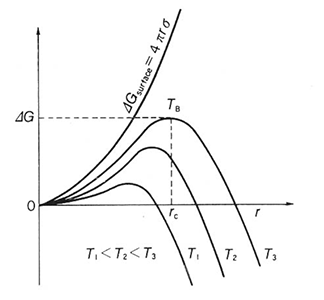図17　球状（半径ｒ）のエンブリオを形成したときのギブズエネルギーと半径との関係 （温度が高いほど，臨界核サイズおよび障壁エネルギーは大きくなる）

図17に示すように温度の上昇とともにおよびは大きくなる。以上の障壁エネルギーをもつ場合の核生成速度（核生成頻度，単位時間に形成される核の数）Iは，

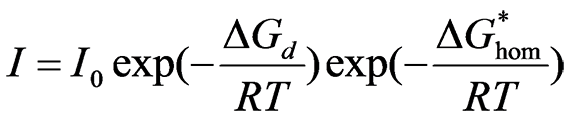(21)

で与えられる。ここで、は原子の拡散の活性化エネルギー、Rはガス定数である．Iは式(21)に示されるように温度によって変化する。に関するexpの項は高温ほど大きくなり（拡散が速くなる）、一方、に関するexpの項は逆に高温ほど小さくなり（障壁エネルギーが大きくなる）、両者の兼ね合いから、ある特定の温度で核生成速度Iは最大となる。これを図18に示す6)．核生成速度Iの時間依存性から，析出の開始時間（あるいは，ある一定量の析出がおこるのに要する時間）は，Iが大きいほど短くなることから，図19のようになる。ここで、図19に示すように析出が最も早くおこる温度はノーズ温度とよばれ、また、曲線形状がC字型になっていることから、これはC曲線と呼ばれる。C曲線はTTT曲線（Time-Temperature-Transformation曲線）とも呼ばれる。

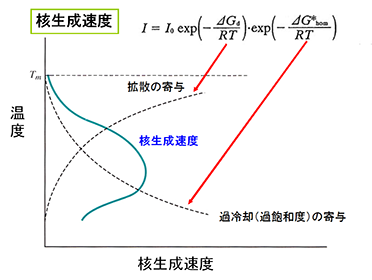図18　核生成速度（核生成頻度）の温度依存性6)

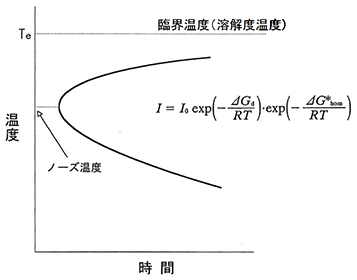図19　析出のC曲線（TTT曲線） 　　　Te：臨界温度（溶解度温度）

(a-2)不均一核生成
核生成が格子欠陥、結晶粒界、介在物、界面などで起こる場合を不均一核生成という。β相がα相中に不均一核生成する例を図20に示す。それぞれの場合の障壁エネルギーはに比べて小さくなる。従って、不均一析出は均一析出よりも常に優先的におこる。

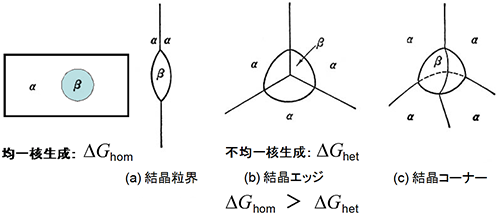図20　粒界における不均一核生成． （不均一核生成の障壁エネルギーは均一核生成の障壁エネルギーより小さい）

 

参考文献
6) J. F. Shackelford: Introduction to Materials Science for Engineers, Prentice-Hall, Inc., (1999), 358.